Genetic Programming
1. Problem
Design and implement a genetic programming system to evolve some perceptrons that match well with a given training set. A training set is a collection of tuples of the form (x1, …, xn, l), where xi’s are real numbers and l is either 1 (positive example) or 0 (negative example). So for your genetic programming system, a ‘program’ is just a tuple (w1, … , wn, θ) of numbers (weights and the threshold). Answer the following questions:
-
What’s your fitness function?
-
What’s your crossover operator?
-
What’s your copy operator?
-
What’s your mutation operator, if you use any?
-
What’s the size of the initial generation, and how are programs generated?
-
When do you stop the evolution? Evolve it up to a fixed iteration, when it satisfies a condition on the fitness function, or a combination of the two?
-
What’s the output of your system for the training set of the below one? Its training-set.csv link
2. Solution
I use Python with Numpy and Pandas.
2.1 Fitness function
This returns the accuracy from 0 to 1 by the number of correctly predicted labels/the number of total labels when X represents the training set as a matrix, y is a vector having a corresponding label set.
def fitness(X, y, genes):
scores = []
y = y.reshape(1, -1)[0]
for g in genes:
sigma = np.matmul(X, g)
a = (sigma >= 0)
b = y.reshape((1, -1))
scores.append(np.sum(a==b) / len(X))
return scores2.2 Crossover operator
This randomly picks two genes from copied top 20% genes and generates a new gene with randomly picking a part of gene from those two until it makes the full gene.
def crossover(high_quality_genes, num_rest_genes):
children = []
while(len(children) < num_rest_genes):
# Create random numbers without redundant
t = np.arange(len(high_quality_genes[0]))
np.random.shuffle(t)
t = t[:2]
# Pick two genes as mother and father randomly with above indices
mother = high_quality_genes[t[0]].copy()
father = high_quality_genes[t[1]].copy()
# Compare each element
compared_element = np.array(mother) == np.array(father)
if np.all(compared_element):
pass
else:
child = []
# randomly pick gene from mother or father for crossover
for i in range(len(mother)):
if np.random.randint(2):
child.append(mother[i])
else:
child.append(father[i])
children.append(child)
return children2.3 Copy operator
It sorts genes by the accuracy and copies top 20% (the first 20% indices) genes.
def copy(rank_index, genes, num_top20):
top20 = rank_index[:int(num_top20)]
return genes[top20]2.4 Mutation operator
It randomly picks one gene and multiplies 1.4 or 0.6 those are randomly chosen number by me.
def mutation(genes):
i = np.random.randint(len(genes))
i2 = np.random.randint(len(genes[0]))
genes[i][i2] *= np.power(-1, i) + 0.4
return genes2.5 The size of the initial generation
def initialise(num_genes, num_weights):
return np.random.uniform(low=-4.0, high=4.0, size=(num_genes, num_weights))
num_genes = 1000
np.random.seed(663)
genes = initialise(num_genes, len(X[0])2.6 The condition of evolution stop
A combination of a fixed iteration and the fitness score. To be specific, the number of iteration is 100 and the score is 0.98 (98% accuracy).
for i in range(100):
# fitness
f = fitness(X, y, genes)
# reversed order index
rank_index = np.argsort(f)[::-1][:]
print('accuracy, [Weights, -Theta]')
print(f[rank_index[0]])
print(genes[rank_index[0]])
print('')
# if top fitness is high enough, stop
if f[rank_index[0]] > 0.98:
break
# copy 20%
high_quality_genes = copy(rank_index, genes, num_genes*0.20)
# create child genes by combining top 20% genes and crossovered
genes[:len(high_quality_genes)] = high_quality_genes
genes[len(high_quality_genes):] = crossover(high_quality_genes, num_genes-len(high_quality_genes))
# mutation
genes = mutation(genes)2.7 Output
accuracy, [Weights, -Theta]
0.8367346938775511
[ 2.71525264 1.11828279 2.68820513 0.27321884 2.52802301 1.8593701
-3.34377527 -2.8875624 1.48904056 -2.05926884]
accuracy, [Weights, -Theta]
0.9387755102040817
[ 1.18220027 -0.46205443 2.75175233 -1.35567167 2.50248339 -0.82743507
-3.70812714 -2.44350959 1.72111065 0.50576898]
accuracy, [Weights, -Theta]
0.9591836734693877
[ 0.33976931 -0.46205443 2.75175233 -0.33115215 2.50248339 -0.82743507
-3.70812714 -2.44350959 1.72111065 0.50576898]
accuracy, [Weights, -Theta]
0.9795918367346939
[-0.84338978 -1.46514636 2.75175233 -1.35567167 3.94876468 1.8593701
-3.70812714 -2.44350959 1.48904056 0.50576898]
accuracy, [Weights, -Theta]
0.9795918367346939
[-0.84338978 -1.46514636 2.75175233 -1.35567167 3.94876468 1.8593701
-3.70812714 -2.44350959 1.48904056 0.50576898]
accuracy, [Weights, -Theta]
1.0
[-0.84338978 -0.46205443 1.18068324 -0.33115215 3.94876468 1.75438933
-3.70812714 -2.44350959 0.73136723 0.50576898]
Final accuracy, [Weights, -Theta]
1.0
[-0.84338978 -0.46205443 1.18068324 -0.33115215 3.94876468 1.75438933
-3.70812714 -2.44350959 0.73136723 0.50576898]
Thus, the final set trains the following perceptron with 100% accuracy.
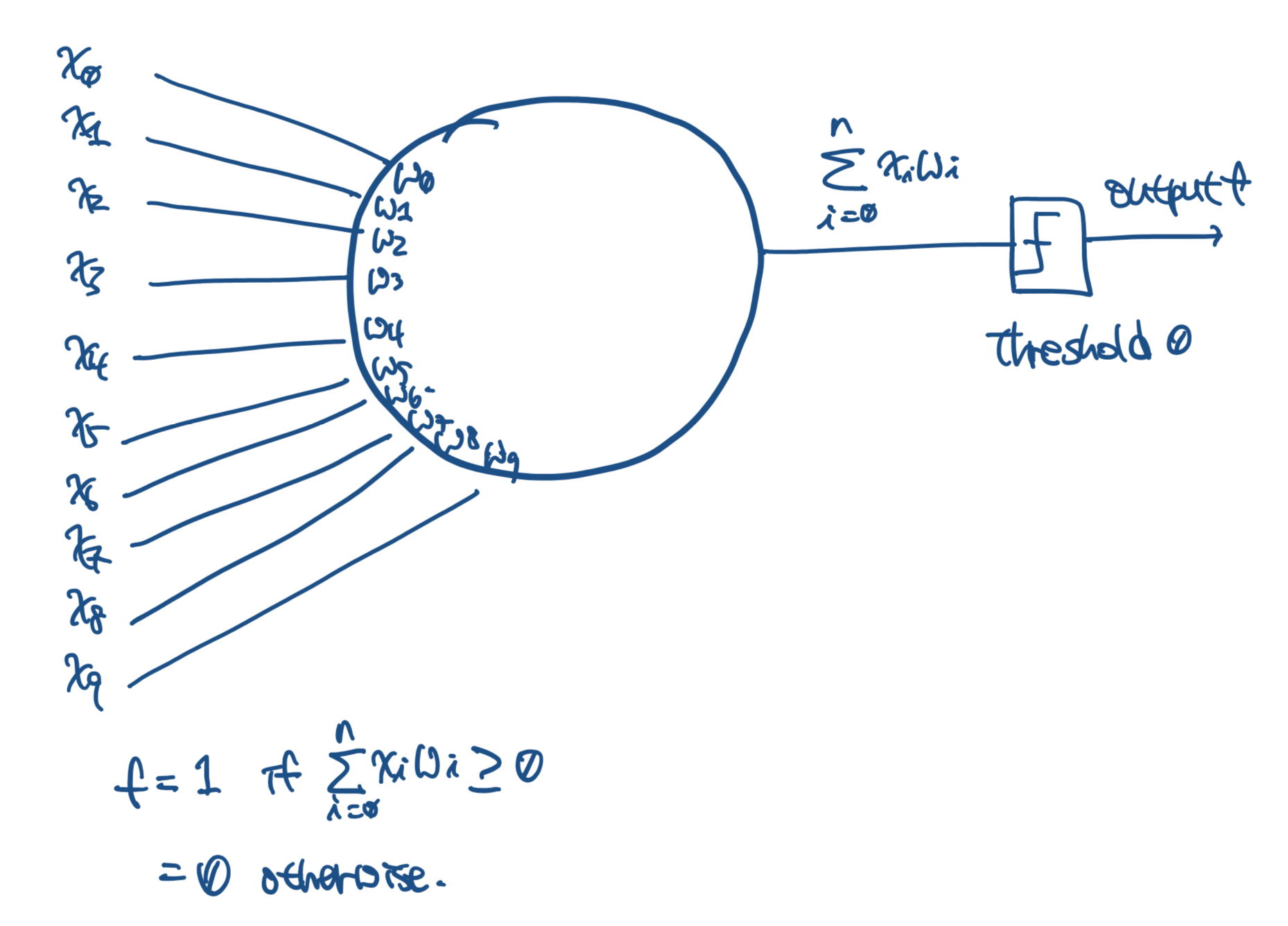
[w0, w1, w2, w3, w4, w5, w6, w7, w8, w9] =
[-0.84338978 -0.46205443 1.18068324 -0.33115215 3.94876468 1.75438933 -3.70812714 -2.44350959 0.73136723 0.50576898]
when x9 = 1 and w9 = -θ
You can check all code here GP.py link Click!.