Apriori Algorithm
1. Problem
Suppose there are 35 candidate item sets of length 3:
{1 2 4}, {1 2 9}, {1 3 5}, {1 3 9}, {1 4 7}, {1 5 8}, {1 6 7}, {1 7 9}, {1 8 9},
{2 3 5}, {2 4 7}, {2 5 6}, {2 5 7}, {2 5 8}, {2 6 7}, {2 6 8}, {2 6 9}, {2 7 8},
{3 4 5}, {3 4 7}, {3 5 7}, {3 5 8}, {3 6 8}, {3 7 9}, {3 8 9},
{4 5 7}, {4 5 8}, {4 6 7}, {4 6 9}, {4 7 8},
{5 6 7}, {5 7 9}, {5 8 9}, {6 7 8}, {6 7 9}
Do write a program to generate a hash tree according to Fast Algorithms for Mning Association, Apriori algorithm, with max leaf size 2 and output the nested list (or nested dict) of the hash tree hierarchically.
For example, the nested list is
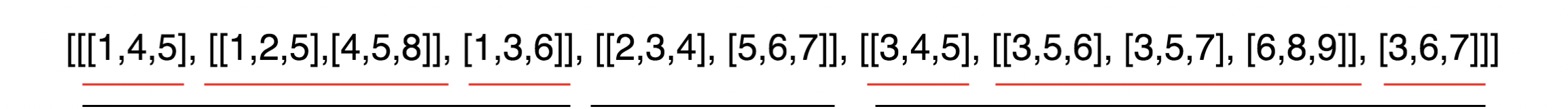
and its corresponding hash tree is
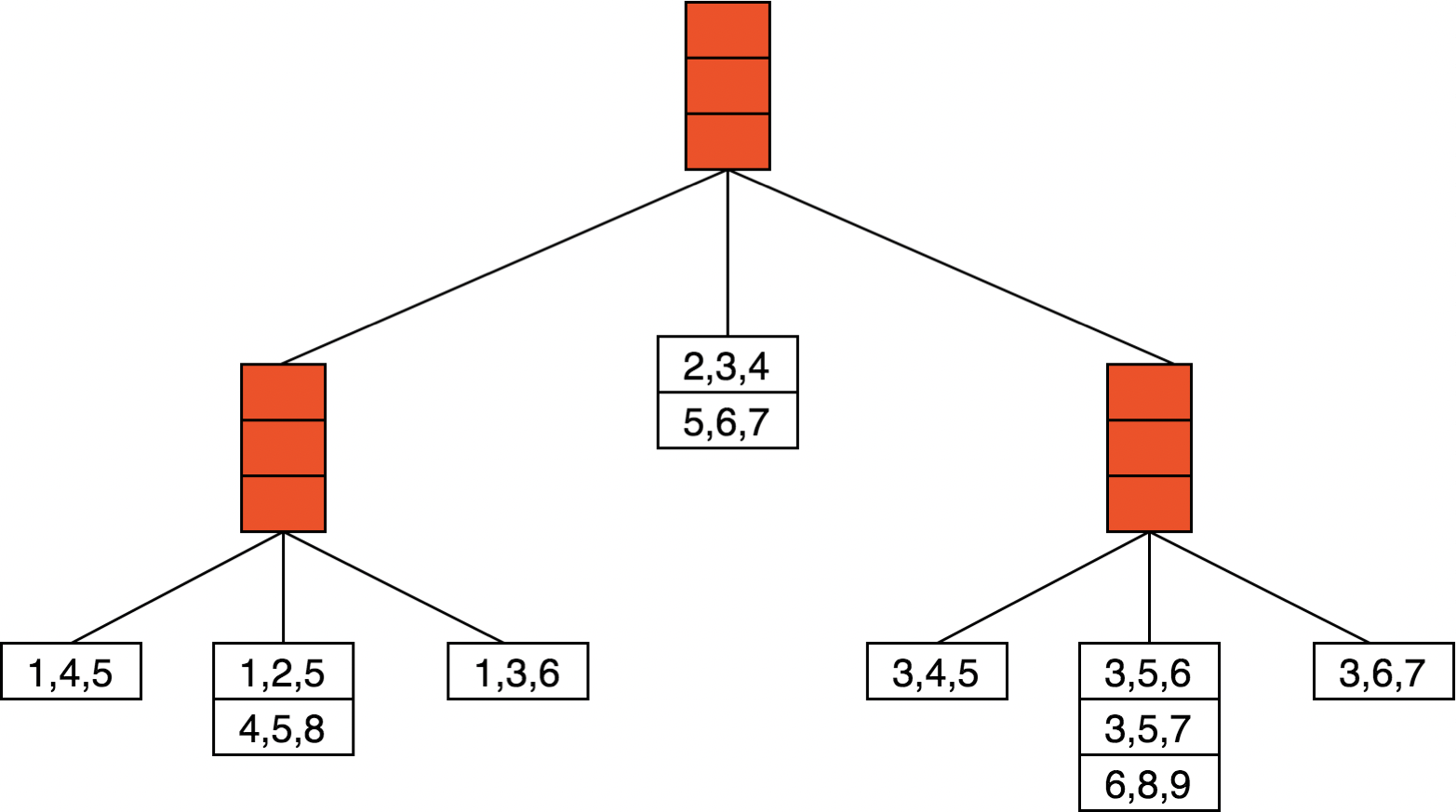
2. Solution
I use Python without any libraries.
def build_tree(tree_type):
tree = tree_type()
itemsets_q1 = [[1, 2, 4], [1, 2, 9], [1, 3, 5], [1, 3, 9], [1, 4, 7], [1, 5, 8]\
, [1, 6, 7], [1, 7, 9], [1, 8, 9], [2, 3, 5], [2, 4, 7], [2, 5, 6]\
, [2, 5, 7], [2, 5, 8], [2, 6, 7], [2, 6, 8], [2, 6, 9], [2, 7, 8]\
, [3, 4, 5], [3, 4, 7], [3, 5, 7], [3, 5, 8], [3, 6, 8], [3, 7, 9]\
, [3, 8, 9], [4, 5, 7], [4, 5, 8], [4, 6, 7], [4, 6, 9], [4, 7, 8]\
, [5, 6, 7], [5, 7, 9], [5, 8, 9], [6, 7, 8], [6, 7, 9]]
# buids a tree
for itemset in itemsets_q1:
tree.add_node(Node(data=itemset))
return treeThe following is my main function to return the result tree and print it out.
hash_tree = build_tree(HashTree)
print(hash_tree)[[[[1, 4, 7], [1, 7, 9], [4, 7, 8]], [[[1, 2, 4], [4, 5, 7]], [[1, 5, 8], [4, 5, 8]], [[1, 2, 9], [1, 8, 9]]], [[[1, 6, 7], [4, 6, 7]], [1, 3, 5], [[1, 3, 9], [4, 6, 9]]]], [[[2, 4, 7], [2, 7, 8], [5, 7, 9]], [[2, 5, 7], [2, 5, 8], [[2, 5, 6], [5, 8, 9]]], [[[2, 6, 7], [5, 6, 7]], [[2, 3, 5], [2, 6, 8]], [2, 6, 9]]], [[[3, 4, 7], [[3, 4, 5], [6, 7, 8]], [[3, 7, 9], [6, 7, 9]]], [[3, 5, 7], [3, 5, 8], [3, 8, 9]], [3, 6, 8]]]
To achieve the above task, I create HashTree class which plays a key role here and implement following functions inside. The max leaf size of a hash tree is fixed as 2, so that I make a hash function first like below (3 is in below code is fixed because of the max size 2 and should be n + 1 for future work to make it flexible).
def hash_func(self, k):
return (k - 1) % 3 The following function finds the proper position to add a node and add it.
def add_node(self, leaf_node):
"""
adds a node into the hash tree
"""
max_leaf_size = 3
itemset = leaf_node.data
node, previous_node, depth, h = self.find_position(itemset=itemset)
self.insert(node, leaf_node, previous_node, depth, h, max_leaf_size)
# delete redundant instance
del leaf_nodeThe following function is to find a suitable position to insert a node according to its hash value. In other words, this is to locate a leaf node which has no children or has list data set, not hash table in a hash tree to add a node.
def find_position(self, depth=0, itemset=None):
node = self.root
# finds a leaf node to add the node
while(type(node.data) == type(self.root.data)):
# calculates hash func of the itemset
h = self.hash_func(itemset[depth])
# updates a hash table in the root
try:
node.data[h].append(itemset)
except KeyError:
# prevents [1, 4, 5, [1, 2, 4]]
# makes [[1, 4, 5], [1, 2, 4]]
node.data[h] = [itemset]
previous_node = node
if h == 0:
node = node.left
elif h == 1:
node = node.middle
else:
node = node.right
# if the node is empty, it should be a leaf one
# so need to break also here
depth += 1
# if a leaf node
if node == None:
return node, previous_node, depth, h
return node, previous_node, depth, hThis is for the node insert in a suitable position by linking the hash tree and the inserted node. There are two cases, need to split or not.
def insert(self, node, leaf_node, previous_node, depth, h, max_leaf_size):
# inserts and links the tree with the added node
try:
node.data.append(leaf_node.data)
if len(node.data) > max_leaf_size:
node = self.split(depth, node)
self.link(h, node, previous_node)
except AttributeError:
# the empty leaf node (node) is assigned to leaf_node(data)
node = leaf_node
# prevents [1, 4, 5, [1, 2, 4]]
# makes [[1, 4, 5], [1, 2, 4]]
node.data = [leaf_node.data]
self.link(h, node, previous_node)When the max size of leaf node reaches more than 3, it should be split.
def split(self, k, node):
new_interior_node = Node(data={})
for itemset in node.data:
h = self.hash_func(itemset[k])
# builds a local hash table
try:
new_interior_node.data[h].append(itemset)
except KeyError:
new_interior_node.data[h] = [itemset]
# adds node
try:
if h == 0:
new_interior_node.left.data.append(itemset)
elif h == 1:
new_interior_node.middle.data.append(itemset)
else:
new_interior_node.right.data.append(itemset)
except AttributeError:
if h == 0:
new_interior_node.left = Node(data=[itemset])
elif h == 1:
new_interior_node.middle = Node(data=[itemset])
else:
new_interior_node.right = Node(data=[itemset])
return new_interior_nodeThe below function is to link the existing node with the added node. This is defined for reuse for cases; Split required or not.
def link(self, h, node, previous_node):
if h == 0:
previous_node.left = node
elif h == 1:
previous_node.middle = node
else:
previous_node.right = nodeI use DFS to print the nested list. You can check all code here HashTree.py link Click!
3. Future Work
- Make code simpler and concise.
- Add a function to draw a hash tree.
- Make it flexible; max leaf size 2 to n.